1603: 【学习系列】二维前缀和
内存限制:128 MB
时间限制:1.000 S
评测方式:文本比较
命题人:
提交:62
解决:26
题目描述
【知识点】
二维前缀和是增对二维数组求前缀和。我们要求二维数组 A 在 $x$ 行 $y$ 列的二维前缀和,计算公式为:$sum_{x,\ y}=\sum_{i=1}^{x} \sum_{j=1}^{y} A_{i,\ j}$。
但是这个公式过于复杂,下面我们通过下图来进一步理解如何计算 $x$ 行 $y$ 列 的二维前缀和。多维前缀和的普通求解方法几乎都是基于容斥原理。
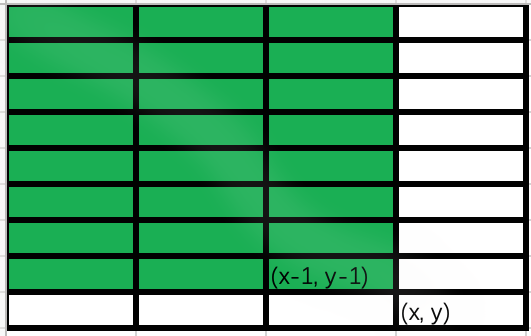
如上图所示,根据前缀和定义,绿色的区域前缀和可以写成 $sum_{x-1,\ y-1}$。

如上图所示,根据前缀和定义,橙色的区域前缀和可以写成 $sum_{x-1,\ y}$。

如上图所示,根据前缀和定义,蓝色的区域前缀和可以写成 $sum_{x,\ y-1}$。
$(x,\ y)$ 这个位置的二维前缀和为 $sum_{x,\ y}$。同时这个位置对应的数据就是 $A_{x,\ y}$,因此我们使用容斥原理。可以得出如下的递推公式。
$sum_{x,\ y}=sum_{x-1,\ y} + sum_{x,\ y-1}-sum_{x-1\, y-1}+a_{x,\ y}$。
【要求】
求一个 $n*m$ 大小的二维矩阵对应的前缀和。
二维前缀和是增对二维数组求前缀和。我们要求二维数组 A 在 $x$ 行 $y$ 列的二维前缀和,计算公式为:$sum_{x,\ y}=\sum_{i=1}^{x} \sum_{j=1}^{y} A_{i,\ j}$。
但是这个公式过于复杂,下面我们通过下图来进一步理解如何计算 $x$ 行 $y$ 列 的二维前缀和。多维前缀和的普通求解方法几乎都是基于容斥原理。

如上图所示,根据前缀和定义,绿色的区域前缀和可以写成 $sum_{x-1,\ y-1}$。

如上图所示,根据前缀和定义,橙色的区域前缀和可以写成 $sum_{x-1,\ y}$。

$(x,\ y)$ 这个位置的二维前缀和为 $sum_{x,\ y}$。同时这个位置对应的数据就是 $A_{x,\ y}$,因此我们使用容斥原理。可以得出如下的递推公式。
$sum_{x,\ y}=sum_{x-1,\ y} + sum_{x,\ y-1}-sum_{x-1\, y-1}+a_{x,\ y}$。
【要求】
求一个 $n*m$ 大小的二维矩阵对应的前缀和。
输入
第一行 $2$ 个正整数:$N$ 和 $M$,$N$ 和 $M$ 范围在 $[1, 1000]$。
其后 $N$ 行,每行 $M$ 个正整数:范围在 $[1, 10000]$。
其后 $N$ 行,每行 $M$ 个正整数:范围在 $[1, 10000]$。
输出
对应二维数组的前缀和。
样例输入 复制
3 4
1 2 4 3
5 1 2 4
6 3 5 9
样例输出 复制
1 3 7 10
6 9 15 22
12 18 29 45