1902: 【数论】卡特兰数

卡特兰数专题（Catalan）

一、什么是卡特兰数？

明安图数，又称卡塔兰数，英文名Catalan$𝐶𝑎𝑡𝑎𝑙𝑎𝑛$ number$𝑛𝑢𝑚𝑏𝑒𝑟$，是组合数学中一个常出现于各种计数问题中的数列。以中国蒙古族数学家明安图 (1692−1763)$(1692-1763)$和比利时的数学家欧仁·查理·卡塔兰 (1814–1894)$(1814–1894)$的名字来命名，其前几项为(从第零项开始) : 1,1,2,5,14,42,132,429,1430,4862,16796,58786…$1,1,2,5,14,42,132,429,1430,4862,16796,58786\dots$

知乎 卡特兰数四连击

https://zhuanlan.zhihu.com/p/31317307
https://zhuanlan.zhihu.com/p/31526354
https://zhuanlan.zhihu.com/p/31585260
https://zhuanlan.zhihu.com/p/31050581

卡特兰数的几何意义

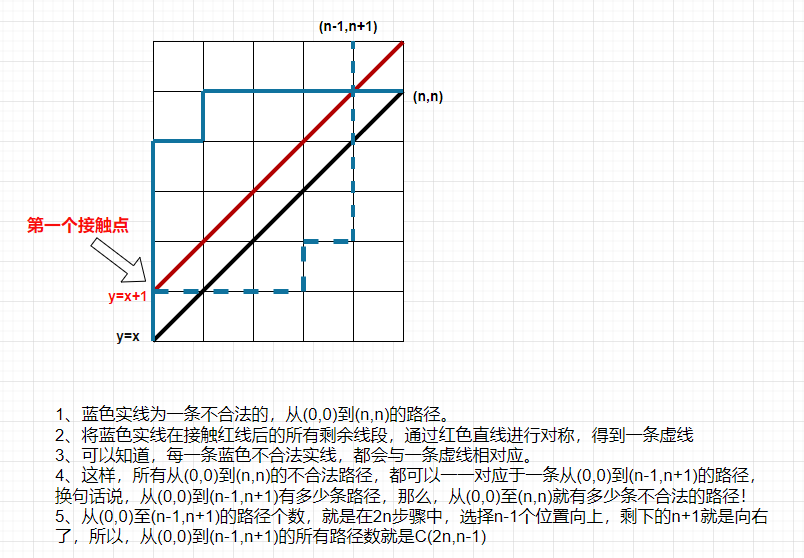
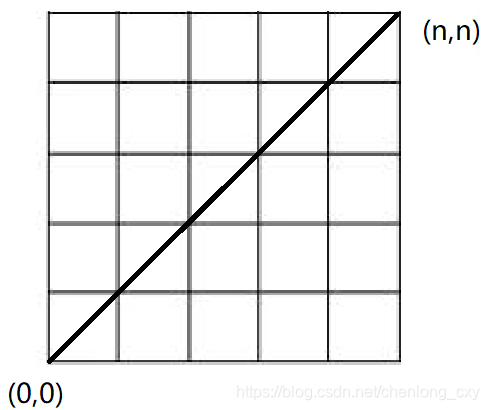
简单来说，卡特兰数就是一个有规律的数列，在坐标图中可以表示为：从原点(0,0)$(0,0)$出发，每次向x$𝑥$轴或者y$𝑦$轴正方向移动1$1$个单位，直到到达(n,n)$(𝑛,𝑛)$点，且在移动过程中不越过第一象限平分线的移动方案总数。

卡特兰数公式推导

我们暂且先不考虑移动过程中不越过第一象限平分线这个约束条件，那么从(0,0)$(0,0)$点到(n,n)$(𝑛,𝑛)$点的过程中，我们总共需要向右移动n$𝑛$步，向上移动n$𝑛$步，一共2n$2𝑛$步。我们可以理解为在2n$2𝑛$步里面选出n$𝑛$步来向上移动，那么剩下的n$𝑛$步就是向右移动的步数，那么方案总数就是Cn2n${\displaystyle {𝐶}_{2𝑛}^{𝑛}}$

现在，我们来看看如何解决不越过第一象限平分线这个问题。仔细想想，不越过第一象限平分线也就等价于不触碰到y=x+1$𝑦=𝑥+1$这条直线。而我们如果把触碰到了直线y=x+1$𝑦=𝑥+1$的路线的第一个与y=x+1$𝑦=𝑥+1$的触碰点之后的路线关于直线y=x+1$𝑦=𝑥+1$对称，并画出对称后的路线

黄海解读

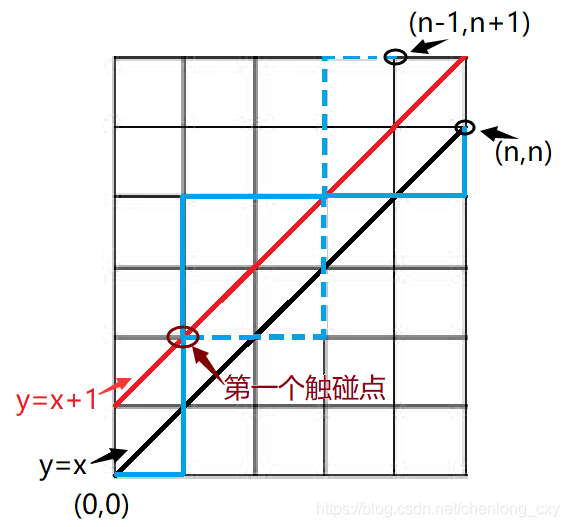
我们会发现触碰到了直线y=x+1$𝑦=𝑥+1$的路径的终点都变成了点(n−1,n+1)$(𝑛-1,𝑛+1)$。也就是说，从(0,0)$(0,0)$点到(n,n)$(𝑛,𝑛)$点的路线当中触碰了直线y=x+1$𝑦=𝑥+1$的路线条数与从(0,0)$(0,0)$点到(n−1,n+1)$(𝑛-1,𝑛+1)$点的路线条数的数量是相等的。于是从(0,0)$(0,0)$点到(n,n)$(𝑛,𝑛)$点的非法路径条数为Cn−12n${\displaystyle {𝐶}_{2𝑛}^{𝑛-1}}$ 。

综上所述，从(0,0)$(0,0)$点到(n,n)$(𝑛,𝑛)$点满足条件的路径数为

卡特兰数通项公式I

$$\huge f(n)=C_{2n}^{n}-C_{2n}$$

---

通过化简，公式可以简化为：

$Catala{n}_n=C_{2n}^n-C_{2n}^{n-1}=\frac{\left(2n\right)!}{n!\times n!}-\frac{\left(2n\right)!}{(n+1)!\times (n-1)!}=\frac{\left(2n\right)!\times (n+1)}{n!\times (n+1)!}-\frac{\left(2n\right)!\times n}{n!\times (n+1)!}=\frac{\left(2n\right)!\times (n+1)-\left(2n\right)!\times n}{n!\times (n+1)!}=\frac{\left(2n\right)!}{n!\times (n+1)!}=\frac{1}{n+1}\times \frac{\left(2n\right)!}{n!\times n!}=\frac{C_{2n}^n}{n+1}$

卡特兰数通项公式II

$f\left(n\right)=\frac{C_{2n}^n}{n+1}$

---

除了这个通项公式之外，卡特兰数还有一个由该通项公式推导而来的递推公式：

Catalann+1=1n+2Cn+12n+2=1n+2×(2n+2)!(n+1)!×(n+1)!=1n+2×(2n)!×(2n+1)×(2n+2)n!×n!×(n+1)2=1n+2×(2n+1)×(2n+2)n+1×1n+1×(2n)!n!×n!=2(2n+1)n+2×1n+1×Cn2n=4n+2n+2Catalann$$\begin{gathered} {\displaystyle 𝐶𝑎𝑡𝑎𝑙𝑎{𝑛}_{𝑛+1}=\frac{1}{𝑛+2}{𝐶}_{2𝑛+2}^{𝑛+1}} \\ =\frac{1}{𝑛+2}\times \frac{(2𝑛+2)!}{(𝑛+1)!\times (𝑛+1)!} \\ =\frac{1}{𝑛+2}\times \frac{(2𝑛)!\times (2𝑛+1)\times (2𝑛+2)}{𝑛!\times 𝑛!\times (𝑛+1{)}^2} \\ =\frac{1}{𝑛+2}\times \frac{(2𝑛+1)\times (2𝑛+2)}{𝑛+1}\times \frac{1}{𝑛+1}\times \frac{(2𝑛)!}{𝑛!\times 𝑛!} \\ =\frac{2(2𝑛+1)}{𝑛+2}\times \frac{1}{𝑛+1}\times {𝐶}_{2𝑛}^{𝑛} \\ =\frac{4𝑛+2}{𝑛+2}𝐶𝑎𝑡𝑎𝑙𝑎{𝑛}_{𝑛} \end{gathered}$$

初始值：f[0] = f[1] = 1

卡特兰数公式III(递推)

$f\left(n\right)=\frac{4n-2}{n+1}f(n-1)$

卡特兰数公式IV(取模常用)

$f\left(n\right)=\frac{\left(2n\right)!}{(n+1)!\times n!}$

卡特兰数公式V(递推)

一般不用来实现，用来推规律

$f\left(n\right)=\sum _{i=0}^{n-1}f\left(i\right)f(n-i-1)$

证明：在n$𝑛$对括号的排列中，假设最后一个括号和第i$𝑖$个左括号匹配。则在第i$𝑖$个左括号之前，一定已经匹配上了(i−1$𝑖-1$)对左括号。如下图，因此，此种情况的数量为f(i−1)∗f(n−i)$𝑓(𝑖-1)\ast 𝑓(𝑛-𝑖)$。(1<=i<=n$1<=𝑖<=𝑛$)最后一个右括号可以1∼n$1\sim 𝑛$个左括号匹配共n$𝑛$种情况。

因此，对i$𝑖$从1$1$到n$𝑛$的情况求和得到f(n)=n−1∑i=0f(i)f(n−i−1)${\displaystyle 𝑓(𝑛)=\sum _{𝑖=0}^{𝑛-1}𝑓(𝑖)𝑓(𝑛-𝑖-1)}$，即可得到递推公式。

二、常见考点

1、 进出栈问题

设栈S$𝑆$的初始状态为空，元素a,b,c,d,e$𝑎,𝑏,𝑐,𝑑,𝑒$依次入栈，以下出栈序列有多少种可能性？注意：这个序列顺序是定的.

重点：归纳法思考，由大及小。

我们这样去想，假设最终的出栈序列可能性用f(n)$𝑓(𝑛)$表示，其中n$𝑛$就是元素的个数。

假设第k$𝑘$个数是最后出栈的数，那么:

• 比它小的前k−1$𝑘-1$个数，肯定已经完成了入栈，出栈操作。因为从逻辑顺序上来讲，它们无法压到k$𝑘$下面去吧。
• 比它大的后n−k$𝑛-𝑘$个数，肯定已经完成了入栈，出栈操作。它们倒是可以压到k$𝑘$下面去，但假设k$𝑘$是最后一个出栈的，它们不能破坏掉假设，也必须提出出栈。

现在，k$𝑘$将原来的问题，划分为两个子问题f(n−k)$𝑓(𝑛-𝑘)$和f(k−1)$𝑓(𝑘-1)$,根据乘法原理，结果就是f(n−k)∗f(k−1)$𝑓(𝑛-𝑘)\ast 𝑓(𝑘-1)$。

k$𝑘$的取值范围是1≤k≤n$1\le 𝑘\le 𝑛$,再根据加法原理：

$f\left(n\right)=\sum _{k=1}^{n}f(n-k)\times f(k-1)$

展开写就是：$f\left(n\right)=f\left(0\right)\times f(n-1)+f\left(1\right)\times f(n-2)+...+f(n-1)\times f\left(0\right)$

代码实现：

f[0] = 1; for (int i = 1; i <= 12; i++) { int fi = 0; for (int j = 0; j <= i - 1; j++) fi += f[j] * f[i - j - 1];
    cout << fi << " ";
} 

P1044 [NOIP2003 普及组] 栈

#include <bits/stdc++.h> using namespace std; typedef long long LL; const int N = 20; int f[N]; int main() { int n;
    cin >> n;
    f[0] = 1; for (int i = 1; i <= n; i++) for (int j = 1; j <= i; j++)
            f[i] += f[j - 1] * f[i - j];
    cout << f[n] << endl; return 0;
} 

2、排队问题

变种（排队问题）：出栈入栈问题有许多的变种，比如n$𝑛$个人拿5$5$元、n$𝑛$个人拿10$10$元买物品，物品5$5$元，老板没零钱。问有几种排队方式。熟悉栈的同学很容易就能把这个问题转换为栈。值得注意的是，由于每个拿5$5$元的人排队的次序不是固定的，所以最后求得的答案要n!$𝑛!$。拿10$10$元的人同理，所以还要n!$𝑛!$。所以这种变种的最后答案为h(n)∗n!$ℎ(𝑛)\ast 𝑛!$。
P1754 球迷购票问题

#include <bits/stdc++.h> using namespace std; typedef long long LL; const int N = 30;
LL f[N]; int main() { int n;
    cin >> n;
    f[0] = 1; for (int i = 1; i <= n; i++) for (int j = 1; j <= i; j++)
            f[i] += f[j - 1] * f[i - j];
    cout << f[n] << endl; return 0;
} 

3、 二叉树构成问题

有n$𝑛$个结点，问总共能构成几种不同的二叉树。

我们可以假设，如果采用中序遍历的话，根结点第k$𝑘$个被访问到，则根结点的左子树有k−1$𝑘-1$个点、根结点的右指数有n−k$𝑛-𝑘$个点。k$𝑘$的取值范围为1$1$到n$𝑛$。讲到这里就很明显看得出是卡特兰数了。

AcWing 1645. 不同的二叉搜索树
没有超过long$𝑙𝑜𝑛𝑔$ long$𝑙𝑜𝑛𝑔$的存储范围的话，可以使用递推;

#include <bits/stdc++.h> using namespace std; typedef long long LL; const int N = 1010, MOD = 1e9 + 7; int n; int f[N]; int main() {
    cin >> n;

    f[0] = 1; for (int i = 1; i <= n; i++) for (int j = 1; j <= i; j++)
            f[i] = (f[i] + (LL)f[j - 1] * f[i - j]) % MOD;

    cout << f[n] << endl; return 0;
} 

AcWing 1317. 树屋阶梯
模拟，按照公式（1）进行模拟，需要使用高精度
黄海的题解

AcWing 1257. 二叉树计数

#include <bits/stdc++.h> using namespace std; const int N = 10010; // 5000*2+10 int primes[N], cnt; bool st[N]; int a[N], b[N]; void get_primes(int n) { for (int i = 2; i <= n; i++) { if (!st[i]) primes[cnt++] = i; for (int j = 0; primes[j] * i <= n; j++) {
            st[i * primes[j]] = true; if (i % primes[j] == 0) break;
        }
    }
} int get(int n, int p) { // n!中p的次数 int s = 0; while (n) n /= p, s += n; return s;
} void mul(int a[], int b, int &len) { int t = 0; for (int i = 1; i <= len; i++) {
        t += a[i] * b;
        a[i] = t % 10;
        t /= 10;
    } while (t) {
        a[++len] = t % 10;
        t /= 10;
    } //去前导0 while (len > 1 && !a[len]) len--;
} int C(int a, int b, int c[]) { int len = 1;
    c[1] = 1; for (int i = 0; i < cnt; i++) { int p = primes[i]; int s = get(a, p) - get(b, p) - get(a - b, p); while (s--) mul(c, p, len);
    } return len;
} void sub(int a[], int b[], int &len) { int t = 0; for (int i = 1; i <= len; i++) {
        t = a[i] - b[i] - t;
        a[i] = (t + 10) % 10;
        t < 0 ? t = 1 : t = 0;
    } while (len > 1 && !a[len]) len--;
} int main() { //加快读入 ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0); get_primes(N - 10); int n;
    cin >> n; int a1 = C(n + n, n, a); int b1 = C(n + n, n - 1, b); // bl下面没有用到，原因是两数相减，我们知道a>b,按着a的长度来就行了 sub(a, b, a1); for (int i = a1; i >= 1; i--) printf("%d", a[i]); return 0;
} 

4、01$01$序列

给出一个n$𝑛$，要求一个长度为2n$2𝑛$的01$01$序列，使得序列的任意前缀中1$1$的个数不少于0$0$的个数,有多少个不同的01$01$序列?

以下为长度为6$6$的序列:
111000 101100 101010 110010 110100

类比一下括号问题，此题就是一个祼的卡特兰数问题。

5、+1$+1$ −1$-1$序列

n$𝑛$个+1$+1$和n$𝑛$个−1$-1$构成的2n$2𝑛$项 a1,a2,⋅⋅⋅,a2n${𝑎}_1,{𝑎}_2,···,{𝑎}_{2𝑛}$ ，其部分和满足非负性质，即a1+a2+⋅⋅⋅+ak>=0，(k=1,2,⋅⋅⋅,2n)${𝑎}_1+{𝑎}_2+···+{𝑎}_{𝑘}>=0，(𝑘=1,2,···,2𝑛)$ ，有多少个不同的此序列?

此典例解析与01$01$序列解析一模一样，即此数列的个数等于第n$𝑛$个Catalan$𝐶𝑎𝑡𝑎𝑙𝑎𝑛$数，此处就不再赘述。

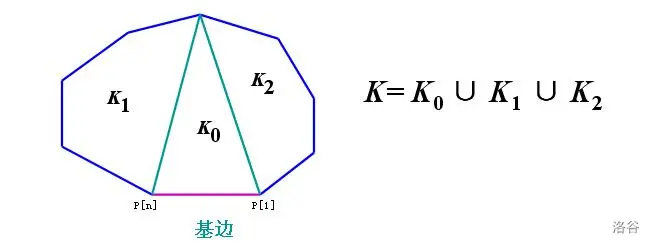
6、凸多边形划分

在一个n$𝑛$边形中，通过不相交于n$𝑛$边形内部的对角线，把n$𝑛$边形拆分为若干个三角形，问有多少种拆分方案？
如五边形有如下5$5$种拆分方案：

如六边形有如下14种拆分方案：

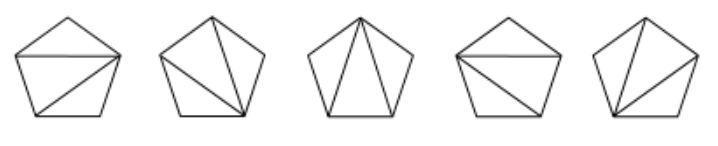
结论：对凸n$𝑛$边形进行不同的三角形分割（只连接顶点对形成n$𝑛$个三角形）数为h[n−2]$ℎ[𝑛-2]$

这也是非常经典的一道题。我们可以这样来看，选择一个 基边 ，显然这是多边形划分完之后某个三角形的一条边。图中我们假设基边是p1,pn${𝑝}_1,{𝑝}_{𝑛}$，我们就可以用 p1,pn${𝑝}_1,{𝑝}_{𝑛}$ 和另外一个点假设为pi${𝑝}_{𝑖}$做一个三角形，并将多边形分成三部分(要是i$𝑖$与1,n$1,𝑛$挨着的话，就是两部分)，除了中间的三角形之外，一边是i$𝑖$边形，另一边是n−i+1$𝑛-𝑖+1$边形。i$𝑖$的取值范围是2$2$到n−1$𝑛-1$。所以本题的解

$c\left(n\right)=c\left(2\right)\ast c(n-1)+c\left(3\right)\ast c(n-2)+...c(n-1)\ast c\left(2\right)$

令f(i)=c(i+2)$𝑓(𝑖)=𝑐(𝑖+2)$则

$f\left(i\right)=f\left(0\right)f(i-1)+f\left(1\right)f(i-2)...+f(i-1)f\left(0\right)$

很明显，这就是一个卡特兰数了。

四、链接资源

五、递推与递归的代码实现

#include <bits/stdc++.h> using namespace std; const int N = 10; // 学习视频 // https://www.bilibili.com/video/BV1nE411A7ST int g[N]; // 递归 int f(int n) { if (n == 0 || n == 1) return 1; int sum = 0; // f(0)*f(n-1)+f(1)*f(n-2)+....+f(n-1)*f(0) for (int i = 0; i < n; i++)
        sum += f(i) * f(n - 1 - i); return sum;
} int main() { // 1、递推法 g[0] = g[1] = 1; for (int i = 2; i < N; i++) for (int j = 0; j < i; j++)
            g[i] += g[j] * g[i - j - 1]; // 考虑思路：画括号法 for (int i = 0; i < N; i++)
        cout << g[i] << endl; // 2 、递归法 for (int i = 0; i < N; i++)
        cout << f(i) << endl; return 0;
} 

__EOF__